8 November 2020
– Policy Brief
Summary of request
Travel-related quarantine regulations are a widely used tool to contain the spread of the pandemic. A quantitative assessment of the associated costs and benefits has not yet been attempted and would be helpful in designing future policy measures.
Executive summary
We simulate economic costs of different COVID-19 quarantine policies in the Swiss context. Our simulations consider pure quarantine measures as well as test-and-release measures. We take into account both indirect effects from higher travel demand when quarantine requirements are relaxed and potential non-adherence to quarantine rules. Epidemiological estimates are used to quantify the additional infection risk from shorter quarantine periods. We express economic costs in terms of economic activity foregone per prevented infection.
Our simulations suggest that there is likely a trade-off: more economic activity through increased travel comes at the cost of more infections. We estimate the costs of the current 10-day quarantine rule relative to having no border measures as between 0.3 and 0.6 million CHF per prevented infection, depending on assumptions. The same costs relative to a test-on-arrival policy are estimated at 0.5 to 1.0 million CHF per infection prevented. When measured against a policy of testing on day 5 after arrival and discharge on day 7 in case of a negative test result, the estimated cost of maintaining the current policy reaches up to 7 million CHF per prevented infection.
In comparison to quarantining based on contact tracing, travel quarantining appears as a relatively costly and ineffective way of reducing infections.
Our simulations are based on the premise that the pandemic is not on an exponential trajectory. If considering a recalibration of quarantine measures, therefore, policy makers should be careful not to imperil the effectiveness of the overall set of measures, especially in times of rising case numbers.
Main text
1. Introduction
In this document, we propose a framework for assessing the epidemiological and economic costs associated with different quarantining models for international travellers, and we provide simulations based on quantifications of the main parameters for Switzerland. At the time of writing, Swiss COVID-19 regulations require inbound international travellers from high-risk countries or regions to quarantine for ten days. The main criterion of “high-risk” has long been case incidence of at least 60/100,000 over 14 days. Since 29 October, this definition has been changed to include only countries whose case incidence exceeds that of Switzerland by 60/100,000 over 14 days. Exceptions have long been made for regions bordering Switzerland and for certain type of travellers (essential workers in health or security, transport staff, participants in sporting or cultural events, participants in professional conferences, etc.). 2 These quarantine requirements can be onerous. At the beginning of October 2020, the list of high-risk origins included 59 countries (among which important travel destinations such as Spain, the United Kingdom and the United States) and 14 regions in neighbouring countries (including important travel destinations such as Paris, the South of France and Vienna). 3 At that time, some 19,000 people were in quarantine after having arrived from one of those countries or regions. During the summer travel season, this number had gone as high as 22,000, but by early November it has fallen to around 3,000. 4 International travel remains severely depressed. For example, the number of landings at Zurich airport was 63% lower in September 2020 than in September 2019. 5 Reduced demand for international travel is due to quarantine requirements but also to people’s reduced willingness to travel even in the absence of the quarantine measures. Data reported by Geneva airport suggest that the imposition of travel quarantine restrictions reduced arrivals from the concerned countries by up to two thirds, from levels that had already been only a fraction of pre-Covid volumes. 6 It is therefore important to evaluate travel-related sanitary measures carefully. Like all evaluations of current policy, with patchy epidemiological as well as economic data, this is an inevitably error-prone undertaking that might need to be revised as new information comes to light. We nonetheless attempt a first quantification, given the importance of the issue for policy and believing that calculations with transparent assumptions should inform decision making. An important caveat applies: our analysis assumes that the effective reproduction rate R e equals one. This has a technical reason, as it simplifies the interpretation and discussion of “infection potential” at the centre of epidemiological simulations. In that sense, the choice is purely presentational. However, this assumption can also be taken as reflecting the fact that our analysis supposes the epidemic to be under control: additional infection risks have finite costs as they do not threaten an unmanageable explosion of cases. We therefore consider a health-wealth trade-off for one particular policy measure without contradicting the view that at the aggregate level and especially during exponential growth of infections, a trade-off between epidemiological and economic costs no longer exists. 7 In our view, the overall policy aim is to protect people’s health and the healthcare system with the least possible disruption to society and the economy. This is best achieved by keeping case numbers low with measures that are less restrictive and economically costly than less targeted measures. It is to be hoped that more cost-benefit analyses of specific policy interventions will be attempted in the future, so that a broader picture of the relative efficacy across the range of measures becomes possible. This document is structured as follows. In Section 2, we present our methodological framework and numerical calibration. Our main results for simulations without and with indirect effects via responses of travel demand are shown in Section 3, and in Section 4 we report corresponding simulations for quarantine measures related to contact tracing. Section 5 concludes.2. Methodology
2.1. Basic cost-benefit framework
We compare alternative policy options to the current 10-day quarantine rule in terms of epidemiological and economic criteria. The epidemiological criterion is the likely number of secondary infections as some infectors “slip through” into the Swiss population. The economic criterion is a composite of up to three factors: the cost of production foregone through quarantine, the economic cost of impeding international travel and, in the case of adding a testing requirement, of testing. For testing, we consider the RT-PCR tests available at the time of writing. In order to be transparent and clear, we simplify the subsequent presentation and ignore many additional important aspects. The societal and economic costs differ substantially from case to case. In general, business travel is likely to have larger economic benefits than leisure travel. Business activities directly contribute to the economy’s productive output, and foreign business travellers spend more money per day in Switzerland than do leisure travellers. 8 Leisure travel, however, may provide large non-monetary value, in particular for people who are able to meet with relatives and friends. Our analysis does not attempt to separate the various costs and benefits associated with different types of travellers, and instead focuses on a generic international traveller. It also abstracts from the fact that maintaining international transport connections – especially at airports – may itself have systemic relevance for the economy. We build on the analytical framework from Ashcroft et al. (2020). Following their notation, we define s as the likelihood that an arriving traveller is infected with the virus; T as the cost of a measure like quarantine or testing that reduces the likelihood that an arriving traveller infects other people in Switzerland; and F as the fraction of potential travel-related infections in Switzerland that were prevented by these measures. Using this notation, we can separate the infection potential of travellers arriving in Switzerland into three groups: A share (1 − s) of travellers is not infected; a share sF represents infection potential eliminated due to measures such as quarantine and testing; and the remaining share s(1 − F) of infection potential “slips through” into the Swiss population. 9 We are interested in comparing the costs and benefits of two different sanitary measures that differ in their costs T, and in their ability to prevent infections, F. In particular, we denote the cost and effectiveness of the benchmark 10-day quarantine policy with T q and F q , and compare it to an alternative policy with lower costs T p < T q and lower effectiveness F p < F q . In this case, the additional cost of adhering to the stricter benchmark policy q rather than the less onerous policy q per infection thereby prevented is defined by ΔC = (T q − T p )/(s[F q − F p ]), conditional on the effective reproduction rate R e being equal to 1. When ΔC is negative for a policy change that relaxes quarantine requirements,this means that the denominator is negative, i.e., that the policy change presents no trade-off, as it reduces both economic costs and epidemiological risk.2.2. Numerical calibrations
The most challenging part of this exercise is to quantify the different variables of the equation. We make the following assumptions:- s: A study of 5,990 arriving passengers at Geneva airport between July and September 2020 showed 31 of them to have been infected. 10 We therefore set s to 0.005 (≈31/5,990), or 0.5%. 11
- F: The fraction of the infection potential of arriving travellers prevented from spreading in Switzerland is contingent on the policy measure considered. 12 Specifically, this variable depends on the following factors:
- Length of the stay abroad: the shorter the stay, the more likely it is that an infected person is to experience his or her most contagious period after arriving back in Switzerland and the less likely a PCR test soon after arrival is to detect the infection. We assume 7 days as the representative length of stay abroad. 13
- Length of quarantine in the absence of testing: We work with the values of F computed by Ashcroft et al. (2020): 0.999 for 10 days of quarantine (implying that almost no infectious arriving traveller “slips through”), down to 0.43 for 2 days of quarantine.
- Day of testing with test-and-release strategy: While PCR tests are very reliable when applied several days after the moment of infection, they are prone to producing false negatives during the early stages (low sensitivity).
- We work with values of F upon returning from a 7-day trip, taken from Ashcroft et al. (2020): 0.999 for tests on day 8, down to 0.54 for tests on arrival. Like Ashcroft et al. (2020), we assume release of travellers with negative test results two days after the test, based on the observation that it takes some 48 hours for PCR swabs to be analysed and results to be communicated.
- Non-adherence: As pointed out by Ashcroft et al. (2020), respect of quarantine rules is unlikely to be universal and likely to decrease with the length of quarantine. Whereas in our baseline scenario, we assume that everyone respects the quarantine rules, our second scenario assumes that there are two types of non-adherence: “contrarian types”, who do not adhere to quarantine from the start, and “impatient types”, who become more likely to discontinue adherence to quarantine the longer it lasts. Thus, for the t th day of quarantine, F is multiplied by an adherence factor (1 − a) − b(t − 1), where a and b are measures of inbound travellers that are, respectively, contrarian and impatient. We set a = 0.2 and b = 0.02, which implies an adherence of 0.72 for a 5-day and 0.62 for a 10-day quarantine period. In the absence of any empirical data on quarantine adherence, this quantification of adherence is inevitably arbitrary and thus highly speculative. Our interest is therefore on whether and how accounting for non-adherence affects the simulations in a qualitative sense, without giving undue weight to the precise numerical values obtained.
- T: The cost of the border policies is quantified as follows:
- We quantify the cost per day of quarantine as Swiss GDP per capita (entire population) per calendar day. In 2019, this amounted to around 230 CHF. We consider this to be a lower bound, as it quantifies only the direct output loss through quarantining the travellers themselves and considering international travellers as if they were a random sample of the population. To the extent that international travellers consist of a disproportional share of economically active people and/or of business travellers, GDP per worker, about 390 CHF per calendar day, would be the more appropriate measure. On the other hand, this measure would ignore that some people can work also while under quarantine (home office).
- Multiplying quarantine days by some fixed cost factor captures the direct cost of quarantine but ignores the indirect “chilling” effect of quarantine requirements on travel demand and associated activity (travel sector, tourism, business travel). The existence of the quarantine rules discourages trips that would otherwise have been desired, which is an economic cost. To the extent that the risk of infection is higher abroad, this indirect effect acts as an epidemiological benefit. We will simulate a simple and inevitably approximate version of such indirect effects.
- Non-adherence: Travellers infringing quarantine rules might take the form of them returning to work, which would reduce the economic costs. In our baseline simulations, we do not take this possibility into account, as it seems more natural to assume quarantine-breaking to be through informal social contacts than through a premature return to work. However, we also explore the sensitivity of our results to considering non-adherence in terms of premature return to work.
- When considering test-and-release policies, we assume a cost per PCR test of 170 CHF. 14
3. Simulation results
3.1. Direct economic costs only
We show calculations with respect to 100,000 arriving travellers. In all our results tables, the left-hand panels describe the simulated scenarios, the middle panels show simulations assuming full adherence with quarantine rules, and the right-hand panels show alternative simulations in which we assume decreasing compliance with quarantine rules, as described above. The first data row of Table 1 shows that in the benchmark situation of 10 days of quarantine, 100,000 travellers imply an economic loss of 230 million CHF, reflecting our assumption that a day of quarantine implies a loss of output of 230 CHF. In this benchmark scenario, 99.9% of secondary infection will be prevented. When we allow for non-adherence in the way described above, 124 secondary infections will occur even under a 10-day quarantine rule. In the panels below the benchmark case, we first show (in columns labelled ns[1 − F]) how the simulated “leakage” of infection potential changes when quarantine is shortened, be it with or without test-and-release and with or without non-adherence effects. This is the epidemiological risk associated with relaxing the measures. Subsequently, the table also shows (in the columns labelled nT) that the economic costs are reduced through shorter quarantine periods. The third and final column of each panel (labelled ΔC) reflects the economic costs of not relaxing the benchmark model per prevented secondary infection. 15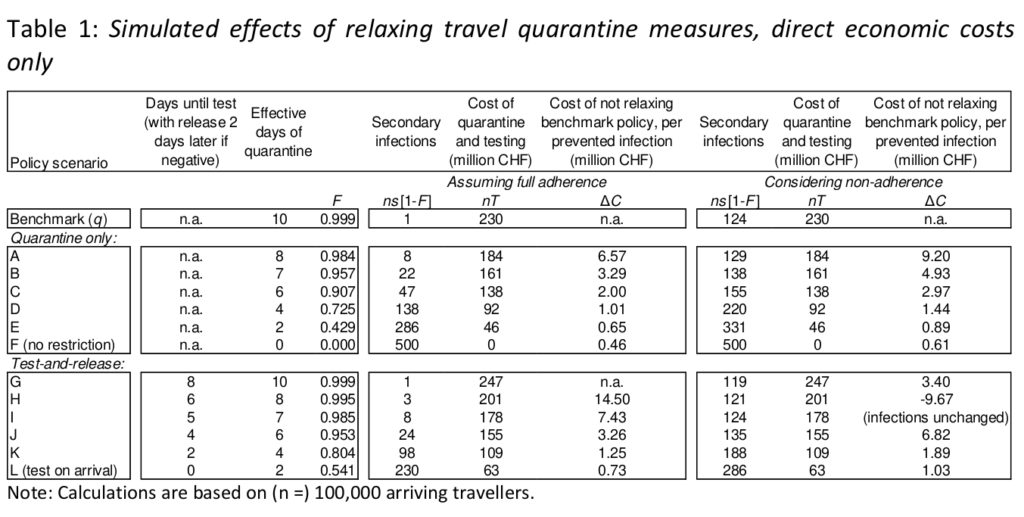
In the basic simulations shown in Table 1, a trade-off appears in most cases between less favourable epidemiological outcomes (more infected travellers released into the Swiss population) and more favourable narrowly defined economic outcomes (lower direct costs from quarantining). In these cases, maintaining the current policy instead of immediately testing inbound travellers on arrival and releasing them from quarantine upon receipt of a negative test result after 2 days (policy scenario L) costs between 0.7 and 1.0 million CHF per prevented secondary infection. Maintaining the current restrictions instead of testing on day 5 of quarantine and releasing (when negative) on day 7 (policy scenario I), implies a cost per prevented infection of 7.4 million CHF, if we assume full adherence.
In our simulations with partial non-adherence, we find that testing on day 5 has no epidemiological cost and considerable economic benefit compared to 10-day quarantine. Testing on day 6 is advantageous in both epidemiological and economic terms – there is no health-wealth trade-off. Further simulations show that the weaker is adherence, the stronger is the case for shortening quarantine. 16
We do not attempt to put a number on the societal value of preventing the release of an infected person into Swiss society. Our simulations in Table 1 offer (conservative) estimates of the economic costs in million CHF per prevented secondary case. Whether these costs are worth paying is a question that depends on the state of the epidemic and on the alternative policy options available.
This analysis is subject to a number of limitations. Our calibrations are inevitably approximate. By working with average values, we miss effects of heterogeneity and dependence across variables. For instance, the daily infection risk may be higher for weekend travellers than for travellers on longer journeys, and weekend travellers may also be less disciplined in complying with quarantine regulations than business travellers. A more detailed modelling effort, including access to relevant data, would be required to capture such effects.
3.2. Direct and indirect economic costs
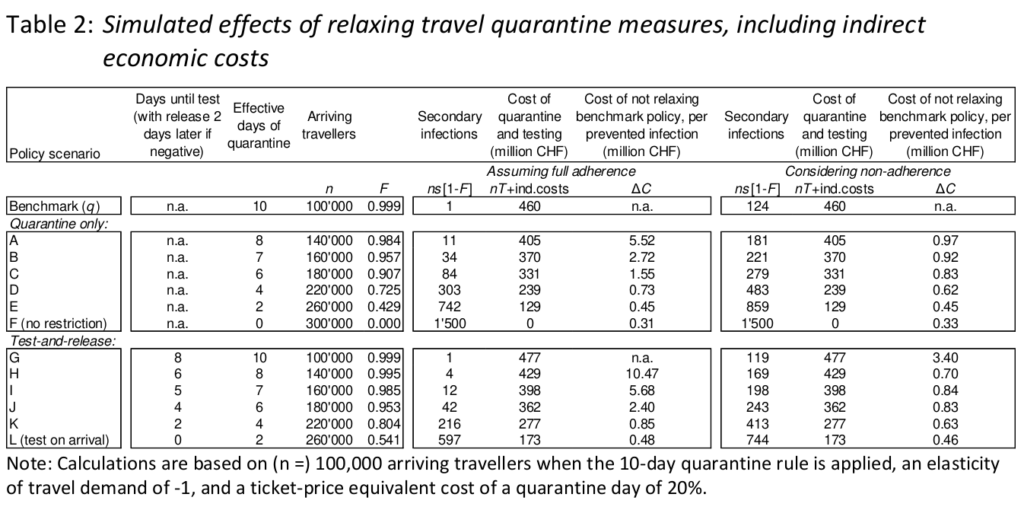
One particularly important limitation is that our framework so far does not account for indirect economic costs associated with reduced demand for travel. A comprehensive evaluation should take into account the value of trips foregone that would have been undertaken in the absence of the quarantine requirements. From an epidemiological point of view, if reducing international travel demand reduces the probability of being infected this is beneficial. In purely economic terms, however, impeding international travel also has costs.
Quantifying indirect economic costs requires estimates of at least two variables: the number of trips that did not take place because of the quarantine, and the average value of such trips. Any foregone journeys could have taken place for three different reasons. First, they could have taken place in the context of business-to-business relationships, where representatives of the foreign country would have travelled to Switzerland, or the other way around. Either way, both parties, probably to different degrees, bear a cost from the implied higher cost of business travel. To the extent that it concerns foreign workers travelling to Switzerland, this also directly affects the Swiss hospitality sector. 17 Second, Swiss residents might have travelled abroad for leisure. The foregone utility is a cost for Swiss society. In monetary terms, there are likely substitution effects from which the Swiss hospitality sector benefits, through increased domestic demand for hospitality services. Third, foreign tourists will not have entered Switzerland. This entails an economic cost for the Swiss hospitality sector and a utility cost for Swiss residents who are prevented from receiving foreign-based relatives and friends.
For a rough estimate of the number of trips foregone, we consider estimates of the price elasticity of private air travel demand. A conservative estimate of this elasticity is –1, which means that a 1% increase in travel prices leads to a reduction of 1% in the number of trips. 18 Suppose that, from the point of view of the representative traveller, every day of quarantine adds 20% to the effective price this individual pays for the trip. This would mean that a 10-day quarantine requirement multiplies the effective price of travel by 3 and thereby reduces travel demand by 67%. 19 To put a monetary value on trips foregone, we use the standard microeconomic equilibrium condition that marginal cost equals marginal benefit. The marginal indirect cost of an additional day of quarantine, summed across potential travellers, is the cost of that quarantine day, for which we can again take the value of 230 CHF. We then multiply this by the number of trips foregone, at every level of quarantine length. By this rough estimate, the indirect economic cost of the benchmark 10-day quarantine per 100,000 arriving travellers is 230 million CHF (= 200,000 trips foregone x 230 CHF per trip x 0.5). This turns out to equal the direct economic costs of a 10-day quarantine period as reported in Table 1. 20
4. Comparison with contact-tracing quarantine
One way of gauging the effectiveness of travel-related measures is to compare them to quarantining linked to contact tracing. The key variable for such a comparison is s, the share of quarantined individuals who have the virus. According to the one study of international-travel-related transmission we are aware of (following arrivals at Geneva airport), this rate was around 0.5%. This is the value we have used in our simulations of Tables 1 and 2. 22 How does this compare to quarantining through contact tracing? Evidence from Geneva (sample size 7,253) suggests that some 6.9% of traced contacts ended up testing positive within the quarantine period – a rate that is 15 times larger than that observed in the same canton for people quarantined because of arriving from a high-risk region or country. This number, however, combines traced contacts from within the same household and from outside the household. For a comparison with infection rates among quarantined international travellers, it would be more appropriate to consider non-household traced contacts specifically. Such detailed evidence does not yet seem to have been collected in Switzerland, but it exists for some other countries. Not surprisingly, high rates of infection have been found among same-household contacts – some 19% according to a meta study (Madewell et al. 2020). Data on infection rates of non-household contacts established through contact tracing are sparse and noisy. In an overview, Kucharski et al. (2020) report shares between 0% (USA) and 5.3% (Guangzhou, China). One particularly large study, based on 5,706 index cases and 48,481 non-household contacts in Korea, finds that 1.9% of those contacts ended up being tested positive (Park et al. 2020). Since only symptomatic and at-risk contacts were tested, this must be a lower-bound estimate of the true infection rate among traced contacts. The empirical uncertainties notwithstanding, our framework allows us to carry out equivalent simulations for quarantine imposed on traced contacts. We make the bold assumption that 5% of such quarantined persons turn out to be themselves infected. Following Ashcroft et al. (2020), we assume that quarantine through contact tracing starts 3 days after the contact with the index case. In Switzerland, quarantine is typically limited to 10 days, counting from presumed last contact. Given the 3-day delay, this means in this context the benchmark “10-day” quarantine consists of 7 days of effective quarantine. We take estimates of secondary infection rates associated with different policy scenarios from Ashcroft et al. (2020).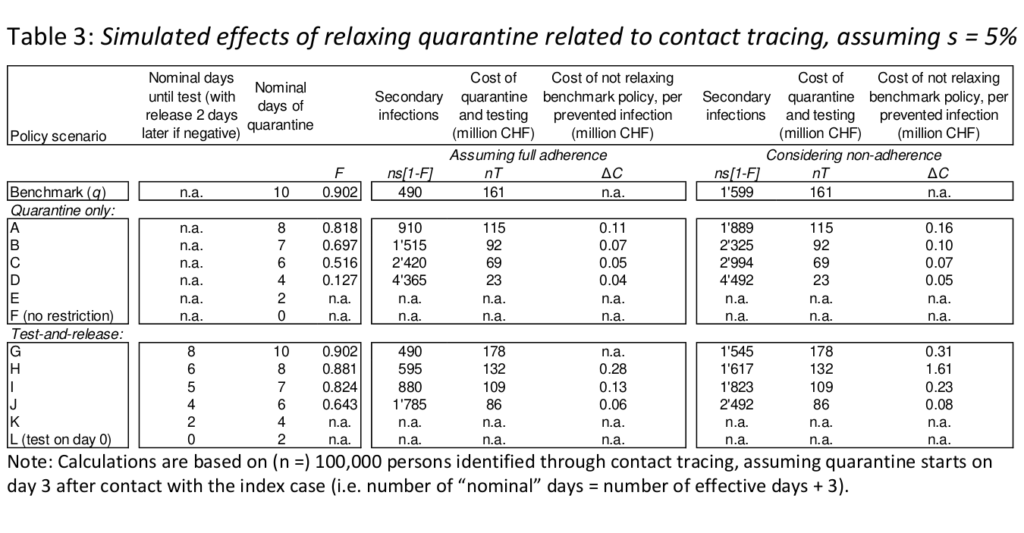
Our simulation results are shown in Table 3. It is apparent from a comparison with Tables 1 and 2 that almost always the higher s attributed to contact tracing quarantine and, to a lesser extent, the lower values for F significantly reduce the economic cost per prevented infection compared to travel quarantine.
Take the example of switching from the benchmark 10-day quarantine policy to a policy of testing on day 5 and releasing on day 7. In the full-adherence simulations of travel quarantine (Table 1, scenario I), this would save 7.4 million CHF per additional secondary infection. Doing likewise for contact-tracing quarantine (Table 3, scenario I), would only save 0.13 million CHF per additional secondary infection. According to these simulations, relaxing contract-tracing quarantine would release a lot more infection potential and save considerably less in terms of economic costs than an equivalent relaxation of travel quarantine.
5. Concluding remarks
Foot notes
1 We thank Sina Streicher for excellent programming support. Peter Ashcroft generously shared detailed simulation results and provided helpful comments together with Sonia Lehtinen. Our Swiss Science Task Force colleagues Sebastian Bonhoeffer, Nicola Low, Richard Neher, Marcel Salathé, Tanja Stadler, Marcel Tanner, Alexandra Trkola and Didier Trono have also contributed valuable input.
2 An exemption exists for work-related trips of up to 5 days. See https://www.admin.ch/opc/en/classified-compilation/20201948/index.html#a4
3 See https://www.admin.ch/opc/en/classified-compilation/20201948/index.html#app1
4 See https://www.bag.admin.ch/bag/en/home/krankheiten/ausbrueche-epidemien-pandemien/aktuelle-ausbrueche-epidemien/novel-cov/situation-schweiz-und-international.html
5 See https://github.com/KOF-ch/economic-monitoring/blob/master/data/ch.zrh_airport.arrivals.csv
6 The numbers reported are as follows. In week 32, just prior to the introduction of quarantine requirements for travellers from Spain, passenger numbers to and from Spain were at 32% of the level observed the same week of 2019. A month later, by week 36 of 2020, that share had fallen to 11%. Similarly, the imposition of a 14-day quarantine requirement by the United Kingdom for passengers arriving from Switzerland in week 35 of 2020 was followed within a month by a drop in passenger volume, expressed in percent of the corresponding volume in 2019, from 22% to 10%. Source: Genève Aéroport (2020).
7 See also Bütler et al. (2020).
8 According to data from Swiss Tourism, the average daily expenditure of a foreign tourist is approximately 165 CHF per day, whereas that of a foreign business traveller is estimated at some 330 CHF per day.
9 A formulation that considers also secondary infections would be sFR e , where R e denotes the effective case reproduction rate. As we work on the assumption that R e = 1, we do not explicitly include this variable.
10 The internal study by the department of health of the canton of Geneva is cited by Bonhoeffer et al. (2020). This is a lower-bound estimate, as only the number of positive tests are considered. However, that consideration also applies to other estimates of s used in our analysis.
11 One could also think of 0.5% as representing the value of s for an origin country with 500 infections per 100,000 residents over 14 days, assuming that arriving travellers have on average spent 14 days in that country and had the same amount of social contact as the average resident of that country.
12 To be precise, F represents the share of infected arriving travellers that are prevented by a given policy measure from spreading the infection in Switzerland, weighted by the infectiousness of those travellers during the quarantine period.
13 We are averaging across very different types of travellers: foreign residents visiting Switzerland as well as Swiss residents returning from abroad, and leisure travellers as well as business travellers. The 7-day scenario we retain is based on an underlying assumption that infection risk is constant over the duration of travellers’ stay abroad, and that the average arriving traveller has been abroad for 14 days. We are not yet aware of data allowing us to validate this assumption empirically.
14 See https://www.bag.admin.ch/bag/en/home/das-bag/aktuell/medienmitteilungen.msg-id-79584.html. We do not consider operational details of testing, and in our estimation of indirect effects we implicitly assume tests to be free for incoming travellers. We note, however, that there might be operational efficiency and adherence gains from testing travellers at the point of entry (airport, border crossings), or at least giving them the option to do so. If the cost of tests were charged to the travellers, our estimated indirect effects of shortening quarantine (Table 2) would be somewhat smaller.
15 Technically, policy scenario G is not a relaxation but a policy tightening.
In Appendix Table A.1, we show corresponding simulations in which it is assumed that half of the non-adhering persons return to work. Not surprisingly, this somewhat lowers the economic costs of quarantine, but it does not change the qualitative results. In Appendix Table A.2, we assume strong non-adherence (30% “contrarian types” + 10% “impatient types” dropping out per day of quarantine), and we find that even a policy of testing on day 2 and releasing on day 4 dominates the benchmark policy in both epidemiological and economic terms.
17 Note that Swiss travel quarantine regulations as they were at the beginning of October include some exceptions for returning travellers whose trips did not exceed 5 days and could not be postponed “for compelling professional or medical reasons”. See: https://www.admin.ch/opc/en/classified-
compilation/20201948/index.html#a4
18 See Brülhart et al. (2020).
19 The percentage drop in demand from replacing policy q by policy p is given by (1 − (exp(lnZq + (Zp − Zq)xE))/Zq)xZq/100, where Z is the representative price of a trip and E is the elasticity of international travel demand relative to the price of international travel. Note that the simulated two-thirds reduction in travel volume roughly corresponds to the drop observed at Geneva airport after the introduction of travel quarantine requirements.
20The multiplication by 0.5 is because we consider only trips foregone at every increment of quarantine duration – akin to the “consumer surplus” area below the demand curve.
21 In Appendix Table A.3, we show that assuming an elasticity of travel demand of -2 somewhat reduces the simulated costs, but does not change the qualitative results. An elasticity of -2 is the lower-bound estimate for the most elastic segment of international airline travel (short-haul economy class) found in the review of the empirical literature (Brülhart et al., 2020).
22 Another computation can be made based on the threshold in force to determine “high-risk” countries or regions. If we take the current rule of quarantining arrivals from countries with at least 60 new cases per 100,000 persons within 14 days, and assume that the average arriving traveller has spent 7 days in that country and had the average amount of contacts typical of the country, then the probability that such an arriving traveller will have been infected equals 0.03% (=30/100,000). If we take the extreme case of Israel, where cases per 100,000 over 14 days peaked around 900 in September 2020, this share was equal to 0.45% (=450/100,000). Comparing these percentages to the 0.5% infected observed among quarantined international arrivals in Geneva suggests that the Geneva sample of international travellers was more prone to infection than the average local person in the relevant foreign country. It also suggests that by raising the threshold defining “high-risk” countries or regions, and linking it to the corresponding infection rate in Switzerland, travel-related quarantine would become better targeted (i.e. s would rise).
23 This has not yet happened, see Nadeau et al. (2020).
Ashcroft, P., Lehtinen, S., Angst, D.C., Low, N. & S. Bonhoeffer 2020. Quantifying the impact of quarantine duration on COVID-19 transmission. medRxiv preprint. https://doi.org/10.1101/2020.09.24.20201061
Bonhoeffer, S., Low, N. and other task force members 2020. Considerations regarding the duration of quarantine for people with possible exposure to SARS-CoV-2 infection, draft Policy Brief, Swiss National COVID-19 Science Task Force
Brülhart, M., Cocker, F., Rohner, D. & P. Thalmann 2020. Introducing an airline tax in Switzerland: estimated effects on demand. E4S Policy Brief, University of Lausanne and EPFL. https://e4s.center/document/policy-brief-air-ticket-tax/
Bütler, M. et al. 2020. Is there a health-wealth trade-off during the COVID-19 crisis? Policy Brief, Swiss National COVID-19 Science Task Force.
Genève Aéroport 2020. Rapport passagers réalisés par pays et catégorie Cov19. Internal report.
Kucharski, A.J., Klepac, P., Conlan, A.J.K., Kissler, S.M., Tang, M., Fry, H., Gog, J.R. & W.J. Edmunds 2020. Effectiveness of isolation, testing, contact tracing and physical distancing on reducing transmission of SARS-CoV-2 in different settings: a mathematical modelling study. https://cmmid.github.io/topics/covid19/reports/bbc_contact_tracing.pdf
Madewell, Z.J., Yang, Y., Longini Jr., I.M., Halloran, E. & N.E. Dean 2020. Household transmission of SARS-CoV-2: a systematic review and meta-analysis of secondary attack rate. medRxiv preprint, https://doi.org/10.1101/2020.07.29.20164590
Nadeau, S., et al. 2020. Quantifying SARS-CoV-2 spread in Switzerland based on genomic sequencing data. medRxiv preprint, https://doi.org/10.1101/2020.10.14.20212621
Park, Y.J. et al. 2020. Contact tracing during Coronavirus disease outbreak, South Korea, 2020. Emerging Infectious Diseases, 26(10): 2465-2468. https://doi.org/10.3201/eid2610.201315
Swiss Federal Council, Ordinance on Measures to Combat the Coronavirus (COVID-19) in International Passenger Transport, Article 4 Exceptions to the quarantine requirement. https://www.admin.ch/opc/en/classified-compilation/20201948/index.html#a4Swiss Federal Council, Ordinance on Measures to Combat the Coronavirus (COVID-19) in
International Passenger Transport, Annex. https://www.admin.ch/opc/en/classified-compilation/20201948/index.html#app1
Swiss Federal Council, press release 24.06.2020, Coronavirus: Federal government to assume test costs, SwissCovid app to start on 25 June. https://www.bag.admin.ch/bag/en/home/das-bag/aktuell/medienmitteilungen.msg-id-79584.html
Swiss Federal Office of Public Health, CoronaVirus: Situation in Switzerland. https://www.bag.admin.ch/bag/en/home/krankheiten/ausbrueche-epidemien-pandemien/aktuelle-ausbrueche-epidemien/novel-cov/situation-schweiz-und-international.html
Date of request: –
Date of response: 8/11/2020 and 12/10/2020
In response to request from: –
Comment on planned updates: –
Expert groups and individuals involved: Economics
Contact persons: Marius Brülhart (marius.brulhart@unil.ch), Jan-Egbert Sturm (sturm@kof.ethz.ch)